Paris, April 6th 2016
Last week I received a patch from Svetlana Shorina PostgresPro about regular expressions and conditions checks in the function responsible for data formatting. Following their Oracle source and PostgreSQL destination types, data needs to be transformed before being inserted into PostgreSQL.
I knew that this part would benefit from being optimized but I always thought that this was a waste of time because, in my experience, most of the migration time is taken by the BLOB/CLOB escaping and this is something that cannot really be optimized. This is why I’ve never done this optimisation work and I was wrong.
Well I decided to reconsider and to make some benchmarks on different kinds of tables and data. I was really surprised, here are the results.
Benchmark environment
The benchmarks was done on a good old server that has had his time with 16 CPUs Intel(R) Xeon(R) CPU E5620 @ 2.40GHz (2 sockets x 4 cores HT). Do not expect huge speed on the results, the number of tuples per seconds can be 2 or 3 times faster or more on modern hardware.
Here are the Ora2Pg settings relative to data export:
- LONGREADLEN = 102400000 (yes there’s 100 MB LOB)
- DATA_LIMIT = 30000 (export will be done by bulk of 30,000 tuples)
- BLOB_LIMIT = 100 (BLOB and CLOB will be exported by bulk of 100 tuples only)
Data is exported to files. The tests will be done using different parallelizing modes:
- -j 8: eight processes to write data to file
- -J 2 -j 4: two processes to extract data from Oracle and four processes to write data to file
- -J 4 -j 3: four processes to extract data from Oracle and three processes to write data to file
Tests are run on the latest release v17.3 and then on same release with Svetlana’s patch.
A simple disk write test of 2 GB gave the following results:
dd if=/dev/zero of=toto bs=8k count=244140
244140+0 records in
244140+0 records out
1999994880 bytes (2.0 GB) copied, 1.9143 s, 1.0 GB/s
Just to know, pg_test_fsync returns:
/usr/pgsql-9.4/bin/pg_test_fsync
open_datasync 11788.099 ops/sec 85 usecs/op
fdatasync 11855.279 ops/sec 84 usecs/op
fsync 10594.905 ops/sec 94 usecs/op
fsync_writethrough n/a
open_sync 11160.430 ops/sec 90 usecs/op
We will not import data into PostgreSQL. Also note that Oracle, Ora2Pg and output files are on the same server and same disks, this is clearly not the best architecture to migrate at full speed but we just want a preview of the speed improvement.
Huge LOB data export
First benchmark is done on a huge table with 216 GB of data and 1,050,006 rows with the following Oracle definition:
SQL> DESC TABLE_TEST1
Name Null? Type
----------------------------------------- -------- ----------------------------
COL1 NOT NULL NUMBER(38)
COL2 VARCHAR2(96)
COL3 NOT NULL DATE
COL4 DATE
COL5 VARCHAR2(765)
COL6 NOT NULL VARCHAR2(300)
COL7 CLOB
COL8 CLOB
COL9 CLOB
COL10 NOT NULL BLOB
COL11 NOT NULL NUMBER(38)
COL12 NOT NULL NUMBER(38)
COL13 NOT NULL VARCHAR2(765)
COL14 NOT NULL VARCHAR2(765)
Here are the duration results in seconds:
| Cores | V17.3 | V17.4b | Gain |
|---|---|---|---|
| -j 8 | 5445 | 5045 | 7% |
| -J 2 -j 6 | 3314 | 3064 | 8% |
| -J 4 -j 3 | 2585 | 2341 | 10% |
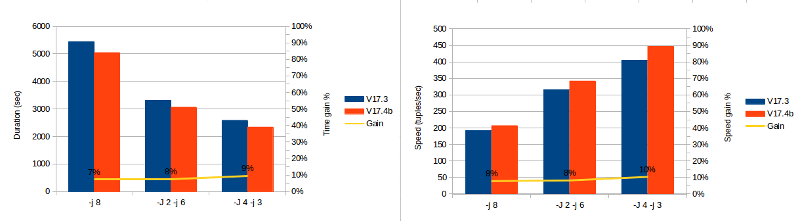
With this kind of table and data types, the speed gain is from 7 to 10 percent. At a maximum speed (447 tuples/sec) it took around 0h45 without the patch and 0h40 with Svetlana’s patch. As expected when you are exporting a table with LOB the gain is not really important but significant enough to be interesting. In this case, the more you can parallelize the data export the more you gain speed.
Small rows, small size
Now let’s make the same tests on a table with small rows (810,000) and small size (1.8GB).
SQL> DESC TABLE_TEST2
Name Null? Type
----------------------------------------- -------- ----------------------------
COL1 NOT NULL NUMBER(38)
COL2 NOT NULL DATE
COL3 NOT NULL CLOB
COL4 NOT NULL NUMBER(38)
COL5 NOT NULL NUMBER(38)
COL6 NOT NULL NUMBER(38)
COL7 NOT NULL NUMBER(38)
COL8 NOT NULL NUMBER(38)
COL9 NOT NULL NUMBER(38)
COL10 NOT NULL VARCHAR2(96)
COL11 VARCHAR2(255)
COL12 NOT NULL VARCHAR2(288)
COL13 NOT NULL VARCHAR2(96)
COL14 NOT NULL CLOB
COL15 NUMBER(38)
COL16 NUMBER(38)
COL17 NUMBER(38)
COL18 NOT NULL VARCHAR2(16)
COL19 DATE
COL20 NUMBER(38)
COL21 NUMBER(38)
COL22 NOT NULL NUMBER(38)
COL23 NOT NULL NUMBER(38)
COL24 NOT NULL DATE
COL25 NOT NULL NUMBER(38)
COL26 NUMBER(38)
COL27 NUMBER(38)
COL28 NUMBER(38)
COL29 NUMBER(38)
COL30 NUMBER(38)
COL31 NUMBER(38)
COL32 NOT NULL NUMBER(1)
And the benchmark results:
| Cores | V17.3 | V17.4b | Gain |
|---|---|---|---|
| -j 8 | 364 | 353 | 3% |
| -J 2 -j 6 | 195 | 195 | 0% |
| -J 4 -j 3 | 113 | 116 | -3% |
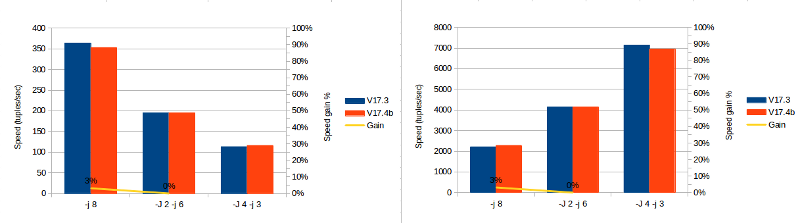
Most of the data are numerics and the majority of data size resides in the CLOB fields. In this case, the patch doesn’t help at all or we need to have a lot more rows to have a noticeable effect.
Table with millions of rows
So until now, there’s nothing really impressive. But now take a look at the results on the following table, which have 28,500,000 rows for just 2.8 GB of data.
SQL> DESC TABLE_TEST3
Name Null? Type
----------------------------------------- -------- ----------------------------
COL1 NOT NULL NUMBER(38)
COL2 NOT NULL NUMBER(38)
COL3 NOT NULL NUMBER(38)
COL4 NOT NULL VARCHAR2(765)
COL5 NOT NULL VARCHAR2(765)
| Cores | V17.3 | V17.4b | Gain |
|---|---|---|---|
| -j 8 | 304 | 207 | 32% |
| -J 2 -j 6 | 276 | 165 | 40% |
| -J 4 -j 3 | 276 | 152 | 45% |
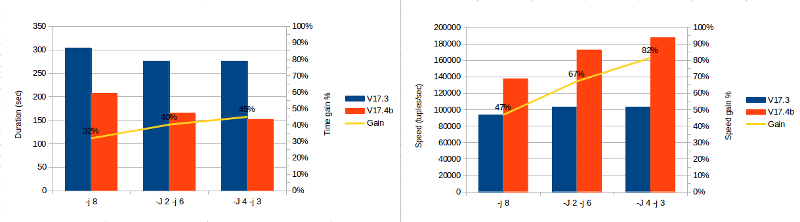
The speed gain is from 32% up to 45% at full speed. The more parallelizing we set, the more speed gain we have. Obviously I was not expecting such a gain, this is a really good news.
Full migration test
I have made a full test on a 500 GB database (380 GB without indexes) where these tables are extracted. This last benchmark has only been done using -J 4 and -j 3 parallelization.
The result is 2h38 (avg: 6059 tuples/sec) with the v17.3 release and only 1h57 (avg: 8183 tuples/sec) with Svetlana’s patch.
This is 26% of time saved for a total of 57,500,000 tuples! This is something really helpful to reduce the migration downtime.
Conclusion
I want to express all my gratitude to Svetlana Shorina and PostgreSQL Professional for this patch. It has already been applied in github development code and will be available in next coming v17.4 release.
Of course the more CPUs you can use, the fastest you can migrate your data, especially for terabytes databases. I think that full database migration performances can be improved by allowing parallel table export (-P) together with parallel data export (-J) for a single table. This is not the case for now, but it is in the TODO list.
